1 Margins
Consider our logistic regression model, where the probability \(p(y=1|x;\theta)\) is modeled by \(g(\theta^T x)\). We predict “1” on an input \(x\) iff \(\theta^Tx\geq0\). That means the larger \(\theta^T x\) is, the larger also is \(p(y=1|x;w,b)\).
Thus, informally, we can think of our prediction as being a very confident one that \(y=1\) if \(\theta^T x >>0\). Similarly, we think of logistic regression as making a very confident prediction of \(y=0\), if \(\theta^Tx<<0\).
Again, informally, it seems that we’d found a good fit for the training data if we can find \(\theta\) so that \(\theta x^{(i)}>>0\) whenever \(y^{(i)}=1\), and \(\theta^T x^{(i)}<<0\) whenever \(y^{(i)}=0\), since this would reflect a very confident (and correct) set of classifications for all the training examples.
Again, informally, it’d be nice if, given a training set, we could find a decision boundary that allows us to make all correct and confident (meaning far from the decision boundary) predictions on the training examples.
2 Notation
We will consider a linear classifier for a binary classification problem with labels \(y\) and features \(x\).
From now on, we’ll use \(y \in \{−1, 1\}\) (instead of \(\{0, 1\}\)) to denote the class labels. We will use parameters \(w,b\) and write our classifier as \[ h_{w, b}(x)=g\left(w^T x+b\right) . \] Here, \(g(z)=1\) if \(z \geq 0\), and \(g(z)=-1\) otherwise.
This “\(w,b\)” notation allows us to explicitly treat the intercept term \(b\) separately from the other parameters.
Our classifier will directly predict either \(1\) or \(−1\) , without first going through the intermediate step of estimating the probability of \(y\) being \(1\) (which was what logistic regression did).
3 Functional and Geometric Margins
3.1 Functional Margins
Functional Margin Definition:
For a training example \((x^{(i)}, y^{(i)})\), the functional margin with respect to a set of parameters \((w, b)\) is defined as: \[ \hat{\gamma}^{(i)}=y^{(i)}\left(w^T x^{(i)}+b\right) \]
This value essentially measures how confident the model is in predicting that a given training example is correctly classified.
Interpretation of Functional Margin:
- If \(y^{(i)} = 1\) , for the functional margin to be large (indicating confidence in the prediction), \(w^T x^{(i)} + b\) needs to be a large positive number.
- If \(y^{(i)} = -1\) , for the functional margin to be large, \(w^T x^{(i)} + b\) should be a large negative number.
- If the product \(y^{(i)} (w^T x^{(i)} + b) > 0\) , it means that the model’s prediction is correct
- A large functional margin indicates that the model is confidently and correctly classifying the example.
- It helps in assessing not just whether the model makes a correct prediction, but also how confident it is about that prediction.
There’s one property of the functional margin that makes it not a very good measure of confidence:
- The classifier function \(g\) (used in predicting \(\pm 1\) ) depends on the sign of \(w^T x + b\) but not on its magnitude.
- scaling \(w\) and \(b\) (e.g., multiplying them by \(2\)) does not change the decision boundary, as the sign of \(w^T x + b\) remains the same.
- Hence, we can make the functional margin as large as we want without changing the underlying classification. (if we scale the parameter, also the functional margin will be scaled) Therefore, the functional margin is not a reliable measure of confidence on its own.
Solution: Normalization
- By normalizing \(w\) and \(b\) (i.e., considering \((w / ||w||_2, b / ||w||_2)\) ), the functional margin becomes a more meaningful measure because it restricts \(w\) and \(b\) from being scaled arbitrarily.
Given a training set \(S=\left\{\left(x^{(i)}, y^{(i)}\right) ; i=1, \ldots, m\right\}\) we also define the function margin of (\(w,b\)) with respect to \(S\) to be the smallest of the functional margins of the individual training examples, denoted by \(\hat{\gamma}\). \[ \hat{\gamma}=\min _{i=1, \ldots, m} \hat{\gamma}^{(i)} \]
3.2 Geometric Margins
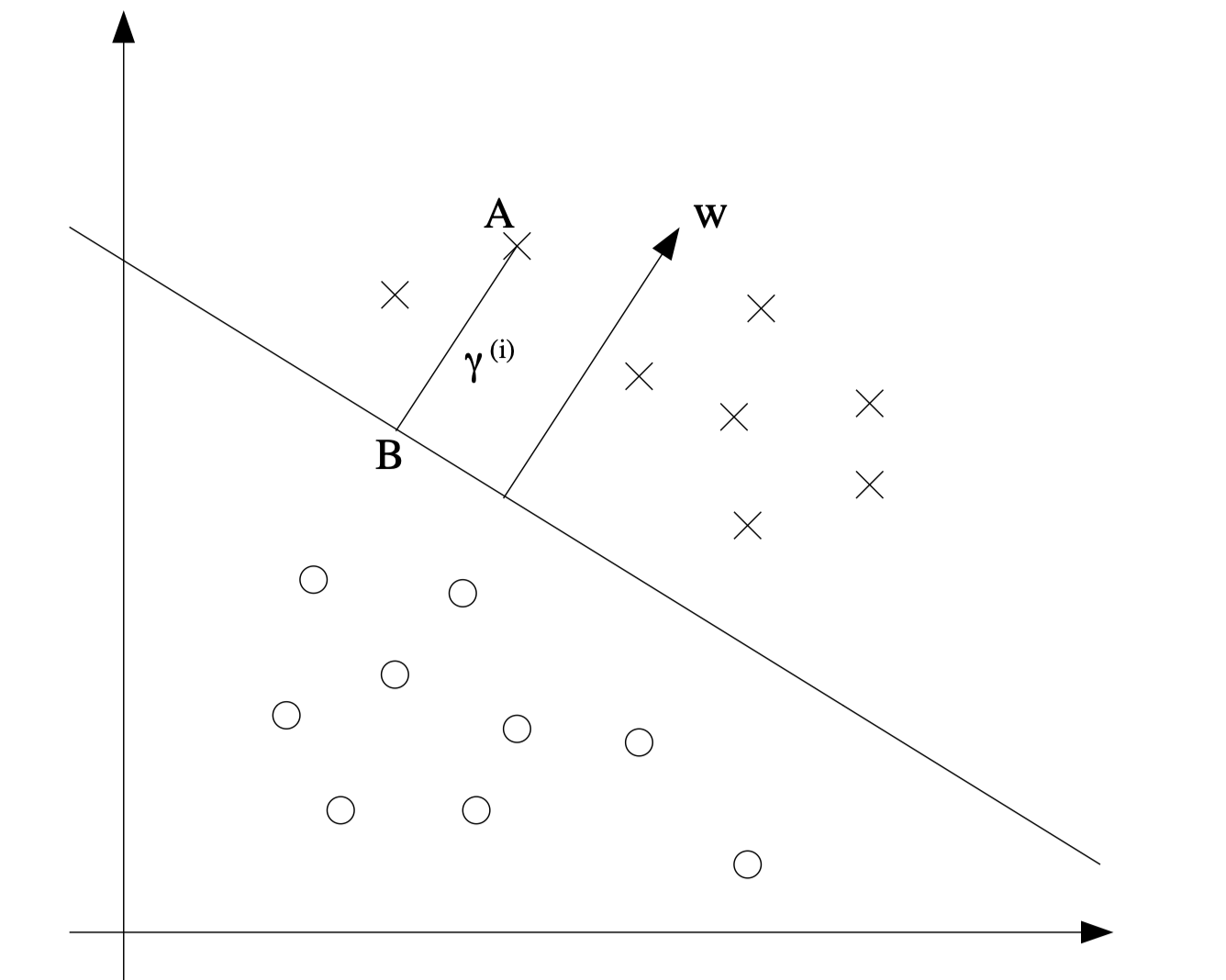
The decision boundary corresponding to \((w,b)\) is shown, along with the vector \(w\). Note that \(w\) is orthogonal to the separating hyperplane.
Consider the point at \(A\). Its distance to the decision boundary, \(\gamma(i)\), is given by the line segment \(AB\).
\(w /\|w\|\) is a unit-length vector pointing in the same direction as \(w\). Since \(A\) represents \(x^{(i)}\), we therefore find that point \(B\) is given by \(x^{(i)}-\gamma^{(i)} \cdot w /\|w\|\). Since \(B\) is on the boundary so \(B\) satisfy the equation \(w^Tx+b=0\). Hence, \[ w^T\left(x^{(i)}-\gamma^{(i)} \frac{w}{\|w\|}\right)+b=0 \] Solving for \(\gamma(i)\) yields \[ \gamma^{(i)}=\frac{w^T x^{(i)}+b}{\|w\|}=\left(\frac{w}{\|w\|}\right)^T x^{(i)}+\frac{b}{\|w\|} . \] More generally, we define the geometric margin of \((w, b)\) with respect to a training example \(\left(x^{(i)}, y^{(i)}\right)\) to be
\[ \gamma^{(i)}=y^{(i)}\left(\left(\frac{w}{\|w\|}\right)^T x^{(i)}+\frac{b}{\|w\|}\right) . \]
- \(\gamma(i)>0\) if the model’s prediction is correct
- if \(\|w\|=1\), then the functional margin equals the geometric margin
- the geometric margin is invariant to rescaling of the parameters
- This invariance allows us to impose any arbitrary scaling constraint on \(w\) without affecting the model’s performance or decision boundary. When fitting w and b to training data, we can choose constraints such as:
- \(||w|| = 1\) (normalizing \(w\) to have a unit norm)
- \(|w_1|\) = 5
- \(|w_1 + b| + |w_2| = 2\)
- These constraints can be satisfied by rescaling \(w\) and \(b\) .
Finally, given a training set \(S=\left\{\left(x^{(i)}, y^{(i)}\right) ; i=1, \ldots, m\right\}\), we also define the geometric margin of \((w, b)\) with respect to \(S\) to be the smallest of the geometric margins on the individual training examples:
\[ \gamma=\min _{i=1, \ldots, m} \gamma^{(i)} \]
4 The Optimal Margin Classifier
From our previous discussion, it is natural to find a decision boundary that maximizes the (geometric) margin, since this would reflect a very confident set of predictions on the training set and a good “fit” to the training data.
Specifically, this will result in a classifier that separates the positive and the negative training examples with a “gap” (geometric margin).
We assume that we are given a training set that is linearly separable; i.e., that it is possible to separate the positive and negative examples using some separating hyperplane.
How we we find the one that achieves the maximum geometric margin? We can pose the following optimization problem: \[ \begin{aligned} \max _{\gamma, w, b} & \gamma \\ \text { s.t. } & y^{(i)}\left(w^T x^{(i)}+b\right) \geq \gamma, \quad i=1, \ldots, m \\ & \|w\|=1 \end{aligned} \] we want to maximize \(\gamma\), subject to each training example having geometric margin at least \(\gamma\).
The \(||w|| = 1\) constraint moreover ensures that the functional margin equals to the geometric margin
But the \(||w|| = 1\) constraint is a nasty (non-convex) one. We transform the problem into: \[ \begin{aligned} \max _{\gamma, w, b} & \frac{\hat{\gamma}}{\|w\|} \\ \text { s.t. } & y^{(i)}\left(w^T x^{(i)}+b\right) \geq \hat{\gamma}, \quad i=1, \ldots, m \end{aligned} \] Here \(\gamma=\hat{\gamma} /||w|\) using the relation of geometric and functional margins. Recall that we can add an arbitrary scaling constraint on $w $ and \(b\) without changing anything (of geometic margins ). We can let \(\hat{\gamma}=1\).
Plugging this into our problem above and noting that maximizing \(\hat{\gamma} /\|w\|=1 /\|w\|\) is the same thing as minimizing \(\|w\|^2\), we now have the following optimization problem:
\[ \begin{aligned} \min _{\gamma, w, b} & \frac{1}{2}\|w\|^2 \\ \text { s.t. } & y^{(i)}\left(w^T x^{(i)}+b\right) \geq 1, \quad i=1, \ldots, m \end{aligned} \]
5 Lagrange Duality
Consider a problem of the following form: